7. COMPUTER GRAPHICS LAB | READ NOW

VTU COMPUTER GRAPHICS LAB

Program 7:- Design, develop and implement recursively subdivide a tetrahedron to form 3D sierpinski
gasket. The number of recursive steps is to be specified by the user.

STEPS TO RUN CG PROGRAM

1. Copy the below copy
2. Past it in any code compiler ex- Code Blocks, DEV C++, VS Code
3. Save the file with .cpp extension
4. Compile and Run the code
5. Program Execution Successful

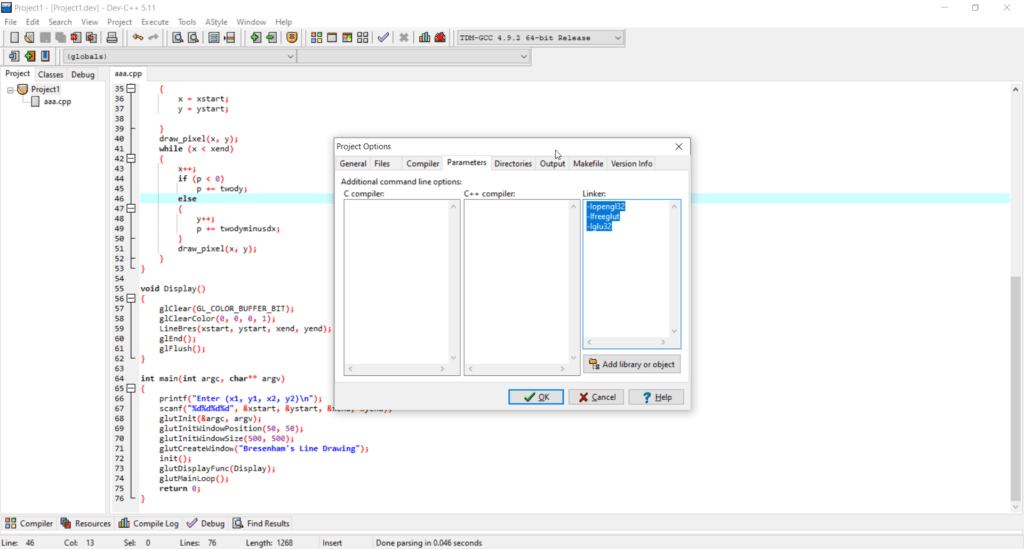
Note:- if you use Dev C++, right click on project>project options>parameter>linker paste the below code in Linker – as shown in image.

-lopengl32
-lfreeglut
-lglu32

Program Code [lab7.cpp]

#include <stdlib.h>
#include <stdio.h>
#include <GL/glut.h>

typedef float point[3];
point v[]={ {0.0, 0.0, 1.0},
			{0.0, 0.942809, -0.33333}, 
			{-0.816497, -0.471405, -0.333333},
			{0.816497, -0.471405, -0.333333}};
static GLfloat theta[] = {0.0,0.0,0.0};
int n;

void triangle( point a, point b, point c)
{
	glBegin(GL_POLYGON);
	glNormal3fv(a);
	glVertex3fv(a);
	glVertex3fv(b);
	glVertex3fv(c);
	glEnd();
}

void divide_triangle(point a, point b, point c, int m)
{
	point v1, v2, v3;
	int j;
	if(m>0)
	{
		for(j=0; j<3; j++)
			v1[j]=(a[j]+b[j])/2;
		for(j=0; j<3; j++)
			v2[j]=(a[j]+c[j])/2;
		for(j=0; j<3; j++)
			v3[j]=(b[j]+c[j])/2;
		divide_triangle(a, v1, v2, m-1);
		divide_triangle(c, v2, v3, m-1);
		divide_triangle(b, v3, v1, m-1);
	}
	else(triangle(a,b,c));
}

void tetrahedron( int m)
{
	glColor3f(1.0,0.0,0.0);
	divide_triangle(v[0], v[1], v[2], m);
	glColor3f(0.0,1.0,0.0);
	divide_triangle(v[3], v[2], v[1], m);
	glColor3f(0.0,0.0,1.0);
	divide_triangle(v[0], v[3], v[1], m);
	glColor3f(0.0,0.0,0.0);
	divide_triangle(v[0], v[2], v[3], m);
}

void display(void)
{
	glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
	glLoadIdentity();
	tetrahedron(n);
	glFlush();
}

void myReshape(int w, int h)
{
	glViewport(0, 0, w, h);
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	if (w <= h)
		glOrtho(-2.0, 2.0, -2.0 * (GLfloat) h / (GLfloat) w, 2.0 * (GLfloat) h / (GLfloat) w, -10.0, 10.0);
	else
		glOrtho(-2.0 * (GLfloat) w / (GLfloat) h, 2.0 * (GLfloat) w / (GLfloat) h, -2.0, 2.0, -10.0, 10.0);
	glMatrixMode(GL_MODELVIEW);
	glutPostRedisplay();
}

void main(int argc, char **argv)
{
	printf(" No. of Divisions ? ");
	scanf("%d",&n);
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
	glutInitWindowSize(500, 500);
	glutCreateWindow("3D Gasket");
	glutReshapeFunc(myReshape);
	glutDisplayFunc(display);
	glEnable(GL_DEPTH_TEST);
	glClearColor (1.0, 1.0, 1.0, 1.0);
	glutMainLoop();
}

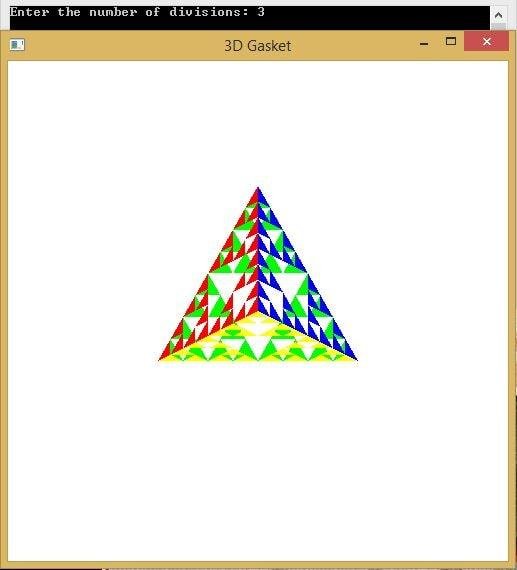
COMPUTER GRAPHICS OUTPUT

Alternative Method [lab7.cpp]

#include<stdio.h>
#include<math.h>
#include<iostream>
#include<GL/glut.h>
using namespace std;
float v[4][3] = { { 0.0,0.0,1.0 },{ 0,1,-1 },{ -0.8,-0.4,-1 },{ 0.8,-0.4,-1 } };
int n;

void triangle(float a[], float b[], float c[])
{
	glBegin(GL_POLYGON);
	glVertex3fv(a);
	glVertex3fv(b);
	glVertex3fv(c);
	glEnd();
}

void divide_triangle(float a[], float b[], float c[], int m)
{
	float v1[3], v2[3], v3[3];
	int i;
	if (m>0)
	{
		for (i = 0; i<3; i++) v1[i] = (a[i] + b[i]) / 2;
		for (i = 0; i<3; i++) v2[i] = (a[i] + c[i]) / 2;
		for (i = 0; i<3; i++) v3[i] = (b[i] + c[i]) / 2;
		divide_triangle(a, v1, v2, m - 1);
		divide_triangle(c, v2, v3, m - 1);
		divide_triangle(b, v3, v1, m - 1);
	}
	else (triangle(a, b, c));
}

void tetrahedron(int m)
{
	glColor3f(1.0, 0.0, 0.0);
	divide_triangle(v[0], v[1], v[2], m);
	glColor3f(0.0, 1.0, 0.0);
	divide_triangle(v[3], v[2], v[1], m);
	glColor3f(0.0, 0.0, 1.0);
	divide_triangle(v[0], v[3], v[1], m);
	glColor3f(1.0, 1.0, 0.0);
	divide_triangle(v[0], v[2], v[3], m);
}

void display()
{
	glMatrixMode(GL_PROJECTION);
	glLoadIdentity();
	glOrtho(-2.0, 2.0, -2.0, 2.0, -10.0, 10.0);
	glMatrixMode(GL_MODELVIEW);
	glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
	tetrahedron(n);
	glFlush();
	glutPostRedisplay();
}

int main(int argc, char* argv[])
{
	cout << "Enter the number of divisions: ";
	cin >> n;
	glutInit(&argc, argv);
	glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUT_DEPTH);
	glutInitWindowSize(500, 500);
	glutInitWindowPosition(0, 0);
	glutCreateWindow("3D Gasket");
	glutDisplayFunc(display);
	glEnable(GL_DEPTH_TEST);
	glClearColor(1.0, 1.0, 1.0, 1.0);
	glutMainLoop();
	return 0;
}

COMPUTER GRAPHICS Alternative Method Output