Design and Analysis of Algorithm Lab 11 | Read Now

Design and Analysis of Algorithm Lab 11

11] Design and implement in java to find a subset of a given set S={S1, S2,….,Sn} of n positive integers whose SUM is equal to a given positive integer d. For example, if S={1,2,5,6,8} and d=9, there are two solutions {1,2,6} and {1,8}. Display a suitable message, if the given problem instance doesn’t have a solution.

11] Program code

import java.util.Scanner;
import static java.lang.Math.pow;
public class lab11
{
	void subset(int num,int n, int x[])
	{
	int i;
	for(i=1;i<=n;i++)
		x[i]=0;
	for(i=n;num!=0;i--)
	{
		x[i]=num%2;
		num=num/2;
	}
	}

	public static void main(String[] args) 
	{
		int a[]=new int[10];
		int x[]=new int[10];
		int n,d,sum,present=0;
		int j;
		System.out.println("enter the number of elements of set");
		Scanner sc=new Scanner(System.in);
		n=sc.nextInt();
		System.out.println("enter the elements of set");
		for(int i=1;i<=n;i++)
		a[i]=sc.nextInt();
		System.out.println("enter the positive integer sum");
		d=sc.nextInt();
		if(d>0)
		{
			for(int i=1;i<=Math.pow(2,n)-1;i++)
			{
				lab11 s=new lab11();
				s.subset(i,n,x);
				sum=0;
				for(j=1;j<=n;j++)
				if(x[j]==1)
					sum=sum+a[j];
				if(d==sum)
				{
					System.out.print("Subset={");
					present=1;
					for(j=1;j<=n;j++)
						if(x[j]==1)
							System.out.print(a[j]+",");
					System.out.print("}="+d);
					System.out.println();
				}
			}
		}
		if(present==0)
			System.out.println("Solution does not exists");
	}
}

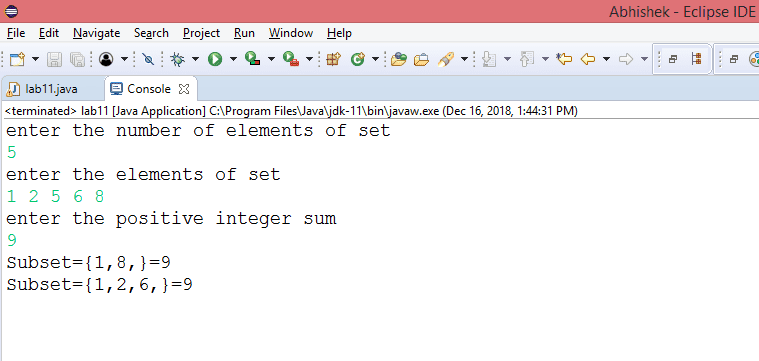
Output